电气控制技术 ¶

​

电机学 ¶

直流电动机 ¶

基本结构：定子 转子

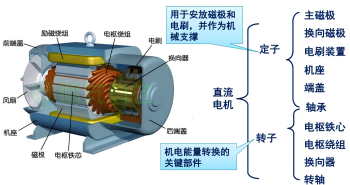
• 注：换向器相邻两片之间相互绝缘

电枢绕组 ¶

• 电枢绕组：转子上的线圈（叠绕组、波绕组、蛙形绕组）

• 绕组元件：两端出线分别和两片换向片 联接的单匝或多匝线圈

• 实槽数：电枢表面所开的嵌线槽，用 Z 表示

• 虚槽数：\(Z_i\) = μZ 同一个槽内放置 μ 元件

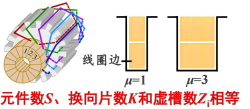
• 元件数 S、换向片数 K 和虚槽数 \(Z_i\) 相等

叠绕组 ¶

• 适用于高电流

• 

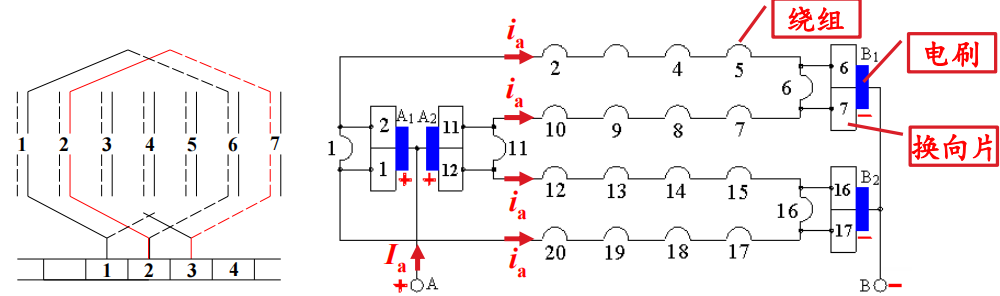
• 单叠绕组的并联支路对数 a 和主磁极极对数 p 相等

• 电枢电流：\(I_a = 2ai_a,其中i_a为每条支路的电流\)

波绕组 ¶

• 高电压（每条支路上电阻多）

• 

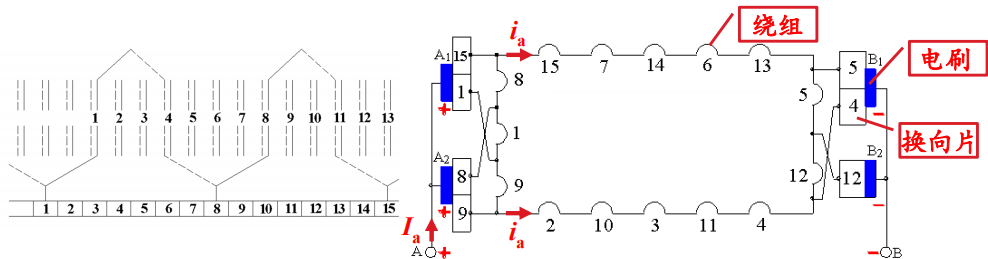
• 单波绕组的并联支路对数 a=1

• 电枢电流：\(I_a = 2ai_a,其中i_a为每条支路的电流\)

励磁方式 ¶

励磁方式是指励磁绕组中励磁电流的获得方式

一共有两套绕组：励磁绕组和电枢绕组

可以理解为电枢绕组先通电，然后通过以下几种方式使得励磁绕组获得励磁电流

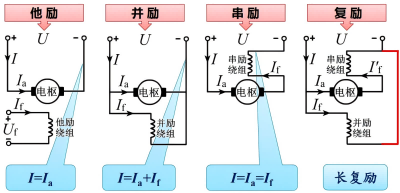
复励分为长复励与短复励：

• 长复励：串励电阻与电枢串后再与并励电阻并
• 短复励：电枢与并励电阻并后再与串励电阻串

直流电动机额定值 ¶

• 额定功率 \(P_N\)
• 额定电压 \(U_N\)
• 额定电流 \(I_N\)
• 额定转速 \(n_N\)
• 额定效率 \(\eta_N\)

\(P_N = U_N I_N \eta_N\)

额定功率是指电动机的输出功率

基本工作原理 ¶

换向器与电刷的共同作用使得外加直流，到电枢内部就变成了交流的形式，实现了持续旋转

感应电动势 ¶

\(每根导体感应的平均电动势: \quad e_{av} =B_{av}lv \\\) \(导体切割磁场线的线速度: \quad v=\frac{2\pi R}{60}n = \frac{2p\tau}{60}n \\\) \(电枢绕组感应电动势: \quad E = \frac{N}{2a}\frac{\Phi}{l\tau}l\frac{2p\tau n}{60} = \frac{pN}{60a}\Phi n = C_e \Phi n \\\) \(其中C_e = \frac{pN}{60a}称为电动势常数\)

电磁转矩 ¶

\(T_{em}=NB_{av}li_a \frac{D_a}{2}\\\) \(T_{em} = N\frac{\Phi}{l\tau}l\frac{I_a}{2a}\frac{2p\tau}{2\pi}=\frac{pN}{2\pi a}\Phi I_a=C_T \Phi I_a\\\) \(C_T=\frac{pN}{2\pi a} 称为转矩常数\)

其中 \(C_T/C_e = 60/2\pi = 9.55\)

并励直流电动机的机械特性 ¶

电路图 ¶

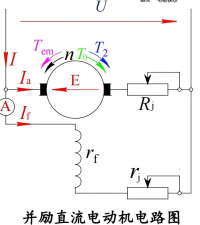
基本方程 ¶

1. 电动势平衡方程

\(U = E+I_a(R_a+R_j)\\\) \(U=I_f(r_f+r_j)=I_fR_f\)

转速公式

\(由E=C_e\Phi n得： n = \frac{U-I_a(R_a+R_j)}{C_e \Phi}\\\)

2. 转矩平衡方程

稳定运行时：\(T_{em} =T_2+T_0 = T_c\) - \(T_c\)为总负载转矩,\(T_2\)为输出转矩 ,\(T_0\)为空载转矩

变速过程 :\(T_{em} =T_2+T_0 + J\frac{d \Omega}{dt} = T_c +\frac{GD^2 dn}{375dt}\) - J为转动惯量，\(GD^2\)为飞轮距

3. 功率平衡方程

输入功率：\(P_1 = UI = U(I_a +I_f)\)

当电枢回路不串外接电阻 \(R_j\) 时：\(P_1 = (E + I_a R_a) I_a + U I_f = E I_a + I_a^2 R_a + U I_f = P_{em} + p_{cua} + p_{cuf}\)

• 其中，\(P_{em}为电磁功率，p_{cua}为电枢回路总损耗，p_{cuf}为励磁回路总损耗\)

电动机的电磁功率：

\(P_{em} = E I_a = T_{em} \Omega = \left(T_2 + T_0\right) \Omega = P_2 + p_0\)

• 其中 \(P_2为输出机械功率，p_0为空载损耗\)

\(p_0 = p_{Fe} + p_{mec} + p_{ad}\)

• 其中 \(p_{Fe}为机械损耗，p_{ad}为附加损耗\)

\(P_1 = p_{\text{cuf}} + p_{\text{cua}} + p_{Fe} + p_{\text{mec}} + p_{\text{ad}} + P_2 = \sum p + P_2\)

• 其中 \(P_2 = P_N\)

机械特性 ¶

机械特性一般表达式：\(n = \frac{U}{C_e \Phi} - \frac{R_a + R_j}{C_e \Phi} I_a = \frac{U}{C_e \Phi} - \frac{R_a + R_j}{C_e C_T \Phi^2} T_{em}\)

并励直流电动机的自然机械特性 ¶

\(n = \frac{U}{C_e \Phi_N} - \frac{R_a + R_j}{C_e \Phi_N} I_a = \frac{U}{C_e \Phi_N} - \frac{R_a + R_j}{C_e C_T \Phi_N^2} T_{em} = n_0 - \beta_N T_{em}\)

$ 其中，Phi_N: 额定运行下的每极有效磁通 quad n_0: 额定电压、额定励磁时所对应的理想空载转速 $

$ beta_N: 自然机械特性的斜率 $

额定负载时转速降越小越好

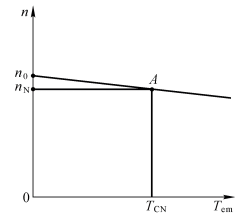
并励直流电动机的人为机械特性 ¶

①改变电枢回路外接电阻 \(R_j\) 的人为机械特性

\(n = \frac{U_N}{C_e \Phi_N} - \frac{R_a + R_j}{C_e C_T \Phi_N^2} T_{em} = n_0 - \beta T_{em}\)

\(R_j\) 越大，斜率也就越大

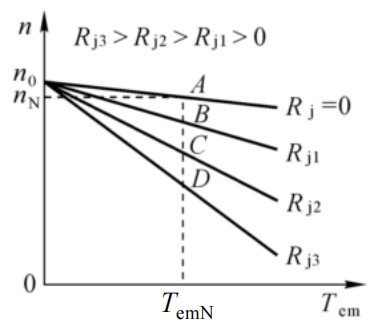
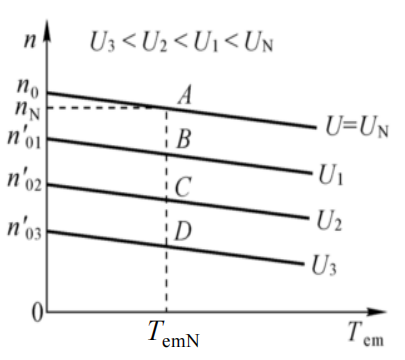
②改变电枢端 U 的人为机械特性

\(n = \frac{U}{C_e \Phi_N} - \frac{R_a}{C_e C_T \Phi_N^2} T_{em} = n_0' - \beta_N T_{em}\)

实际上改变的是空载转速 \(n_0\)

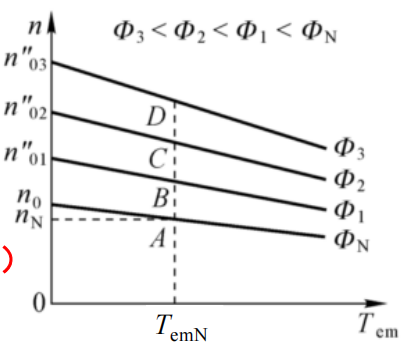
③减弱主磁通 Φ 的人为机械特性 ( 即增大励磁回路外接电阻 \(r_j\))

\(n = \frac{U_N}{C_e \Phi} - \frac{R_a}{C_e C_T \Phi^2} T_{em} = n_0'' - \beta' T_{em}\)

直流电动机的启动、制动与调速 ¶

起动 ¶

存在问题：启动时，n 与 E 均为 0,\(I_a = \frac{U_N - E}{R_a}\) 为额定电流的十几倍以上。

要求：控制起动电流为额定电流的 1.5~2 倍

解决方法：

• 降低电枢端电压起动

起动电压很低，随着 n 的升高，U 也增加

• 电枢回路串电阻起动

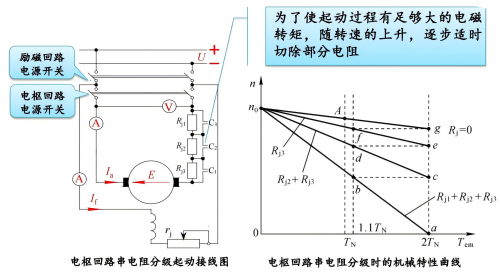
\(I_{st}=I_a = \frac{U_N}{R_a +R_j}\)

随着转速的上升，逐步减小 \(R_j\) 的阻值，实现从 \(a->b->c->e->f->g->A\) 的目标

调速 ¶

• 改变电枢端电压调速（降压调速）

• 改变串入电枢回路电阻调速

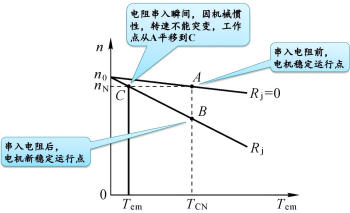
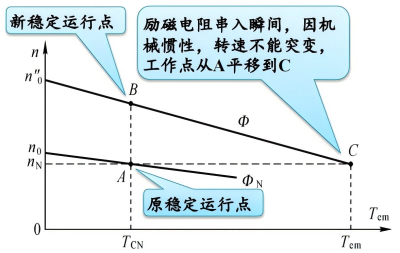
• 改变励磁电流调速（弱磁调速）

不适合恒转矩负载，因为电流会变大，电动机会过热

制动 ¶

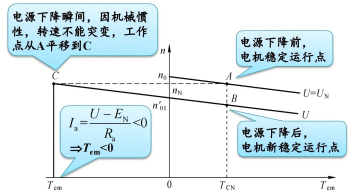
• 能耗制动

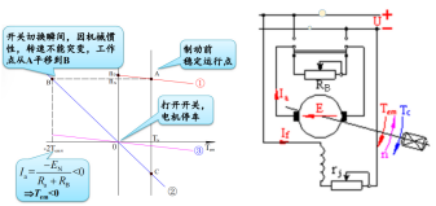
准备制动时，如右图所示，电源断开，不再进行供电，此时 \(n = -\frac{R_a+R_B}{C_e C_T \Phi_N^2}T_{em}\), 因此从线①的 A 点变到线②的 B 点，一般来说需要串联电阻 \(R_B\) 来保护电流，因此从线①的 A 点变到线③。

• 反接制动
• ① 电压反向的反接制动

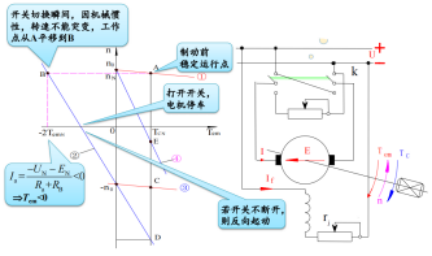
准备制动时，电源电动势反向，此时 \(n = \frac{-U_N}{C_e\Phi_N}-\frac{R_a+R_B}{C_e C_T \Phi_N^2}T_{em}\), 因此，从图中的①线的 A 点变为②线的 B 点

• ② 电势反向的反接制动

上图中，对于位能性负载，即力矩不发生变化，因此会从线①的 A 点慢慢变到线②的 D 点，中间有一时刻转速为 0。

• 回馈制动

变压器 ¶

分类 ¶

• 相数：单相、三相
• 绕组：双绕组、三绕组、多绕组、自耦
• 冷却方式：油浸式、干式
• 铁心结构 ：芯式、壳式

基本结构（非重点）¶

结构：铁心；高、低压两套绕组

铁芯：叠片式、渐开线式 - 其中，叠片式又分芯式和壳式

额定值 ¶

额定容量：\(S_N\)（视在功率 VA） - 原边、副边的额定容量相等

额定电压：原边 \(U_{1N}\), 副边 \(U_{2N}\) - 副边额定电压 \(U_{2N}\) 是变压器原边外加额定电压 \(U_{1N}\) 时副边的空载电压 - 三相变压器，额定电压指线电压

额定电流：原边 \(I_{1N}\), 副边 \(I_{2N}\) - 单相变压器： \(I_{1N} = \frac{S_N}{U_{1N}} \quad I_{2N} = \frac{S_N}{U_{2N}}\) - 三相变压器： \(I_{1N} = \frac{S_N}{\sqrt{3}U_{1N}} \quad I_{2N} = \frac{S_N}{\sqrt{3}U_{2N}}\)

额定频率：\(f_N = 50Hz\)

基本工作原理 ¶

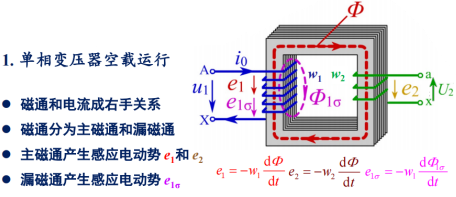
• 若磁通按正弦规律变化，即 \(\Phi = \Phi_msin\omega t \quad e_1 = -w_1 \omega \Phi_m cos\omega t = 2 \pi fw_1 \Phi_m sin(\omega t -90^0)\)
• 用向量表示有 \(\dot{E_1} = -j\sqrt{2}\pi fw_1 \dot{ \Phi}_m = -j4.44 fw_1 \dot{ \Phi}_m\)
• 同理有 \(\dot{E_2} = -j \sqrt{2}\pi fw_2 \dot{ \Phi}_m= -j 4.44 fw_2 \dot{ \Phi}_m\)
• 变压器变比 \(k = \frac{E_1}{E_2}=\frac{w_1}{w_2} \simeq \frac{U_{1N}}{U_{2N}}\)
• \(w_1与w_2为匝数\)

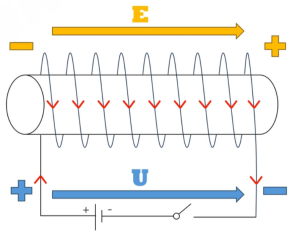
U 和 E 正方向的判定 ¶

视频：变压器 U&E 方向标注

首先考虑一个简单的通电螺线管，将通电的螺线管看作一个电源，电源内部电流从负极流向正级，因此 E 和 U 的方向如下图所示

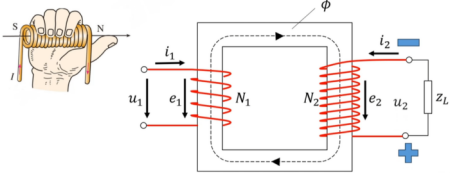
原边的方向与上述通电螺线管判断一致。再根据右手定则判断磁通的方向，如图 \(\phi\) 所示，再根据右手螺旋定则判断副边电流 \(i_2\) 的方向，再根据上面的方法判断 E 和 U 的方向 ,\(U_2\) 由于是负载端，因此 \(U_2\) 的方向与电流方向保持一致。

单相变压器空载运行 ¶

原边等效电路

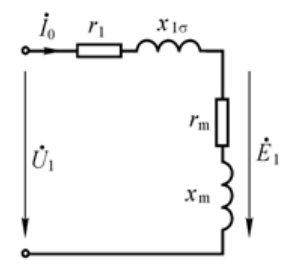
• 原边电动势平衡方程式

\(u_1 = -e_1 - e_{1\sigma} + i_0 r_1\)

\(\dot{U}_1 = -\dot{E}_1 - \dot{E}_{1\sigma} + \dot{I}_0 r_1= -\dot{E}_1 + j\dot{I}_0 x_{1\sigma} + \dot{I}_0 r_1= -\dot{E}_1 + \dot{I}_0 Z_1\)

• 副边电动势平衡方程式

\(u_2=e_2\)

\(\dot{U}_2 = \dot{E}_x\)

单相变压器负载运行 ¶

• 磁动势平衡方程

\(\dot{F}_1=\dot{I}_1 w_1\)

\(\dot{F}_2=\dot{I}_2 w_2\)

\(\dot{F}_1 +\dot{F}_2 =\dot{F}_m=\dot{I}_m w_1\)

• 励磁电流

\(\dot{I}_m = \dot{I}_1+ \frac{w_2}{w_1}\dot{I}_2\)

• 电动势平衡方程式

\(\dot{U}_1 = -\dot{E}_1 - \dot{E}_{1\sigma} + \dot{I}_1 r_1= -\dot{E}_1 + j\dot{I}_1 x_{1\sigma} + \dot{I}_1 r_1= -\dot{E}_1 + \dot{I}_1 Z_1\)

\(\dot{U}_2 = \dot{E}_2 + \dot{E}_{2\sigma} - \dot{I}_2 r_2= \dot{E}_2 - j\dot{I}_2 x_{2\sigma} - \dot{I}_2 r_2= \dot{E}_2 + \dot{I}_2 Z_2\)

折算 ¶

用一个匝数和原边线圈相等的新的副边线圈来替代实际的副边线圈

折算方法：

• 电动势 / 电压的折算值——原值乘以 k
• 电流的折算值——原值除以 k
• 阻抗的折算值——原值乘以 \(k^2\)

折算后的基本方程式 $$ dot{U}{1} = -dot{E}} + dot{I{1} r} + j dot{I{1} x \ dot{U}{2}^{prime} = dot{E}}^{prime} - dot{I{2}^{prime} r}^{prime} - j dot{I{2}^{prime} x \ dot{U}}^{prime{2}^{prime} = dot{I}}^{prime} Z_{L}^{prime} = dot{I{2}^{prime} left(Rright) \ dot{I}}^{prime} + j x_{L}^{prime{1} + dot{I}}^{prime} = dot{I{m} \ dot{E}} = dot{E{2}^{prime} = -j 4.44 f w} dot{Phi{m} \ dot{E}} = dot{E{2}^{prime} = -dot{I}} Z_{m} = -dot{I{m} left(rright) $$ 变压器等效电路图如下图所示} + j x_{m

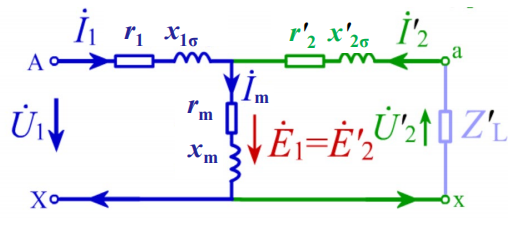
参数测定 ¶

空载实验 ¶

降压变压器：在副边进行空载实验

升压变压器：在原边进行空载实验

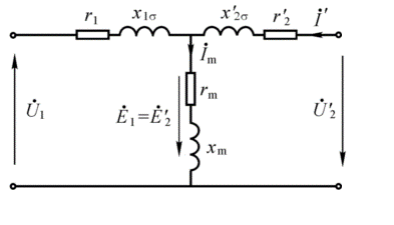
由于 \(Z_m远大于Z_1\)，因此认为 \(U_1\) 与 \(E_1\) 值相等

以降压变压器为例子 $$ z_{2~m} = frac{U_0}{I_0} \

r_{2~m} = frac{p_0}{I_0^2} \

x_{2~m} = sqrt{z_{2~m}^2 - r_{2~m}^2} $$ 三式联立求解，最后则算到原边 $$ z_m = k^2 z_{2~m} \ r_m = k^2 r_{2~m} \ x_m = k^2 x_{2~m} $$

负载实验 ¶

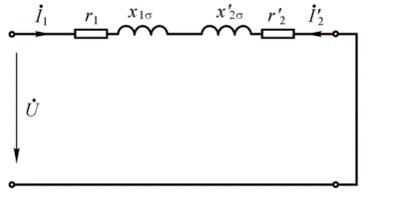
以降压变压器为例子 $$ Z_k = U_k/I_k \ r_k = p_k/I_k^2\ x_k = sqrt{z_k^2-r_k2} $$

外特性与电压变化率 ¶

外特性 ¶

\(U_1 = U_{1N},cos\phi_2=常数时，U_2=f(I_2)\) 的关系曲线称为变压器的外特性

电压变化率（电压调整率）¶

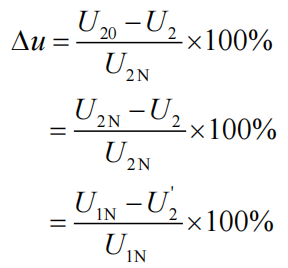
损耗与效率 ¶

基本铜耗：原、副边绕组中电流引起的电阻损耗

附加铜耗：导体在交变漏磁场作用下引起集肤效应，有效电阻增大而增加的铜耗

基本铁耗：铁心中的磁滞和涡流损耗

附加铁耗：结构件中的涡流损耗

异步电机 ¶

异步电动机结构和额定值 ¶

结构 ¶

鼠笼式和绕线式

额定值 ¶

• 额定功率 \(P_N\)
• 额定电压 \(U_N\) （线电压）
• 额定电流 \(I_N\)（线电流）
• 额定转速 \(n_N\)
• 额定效率 \(\eta_N\)

\(P_N = \sqrt{3} U_N I_N cos\phi_N \eta_N\)

各种参数 ¶

槽距角

极距

每级每相槽数