跳转至

[2020]FUEL: Fast UAV Exploration using Incremental Frontier Structure and Hierarchical Planning

约 1183 个字 预计阅读时间 5 分钟

论文资源

IEEE

知乎 1

知乎2

Github源码

主成分分析(PCA)算法

前置知识

PCA 降维

PCA（Principal Component Analysis）是机器学习中常用的一种降维算法，它通过计算样本的协方差矩阵来寻找主成分，并选择主成分个数来降低维度。

Tip

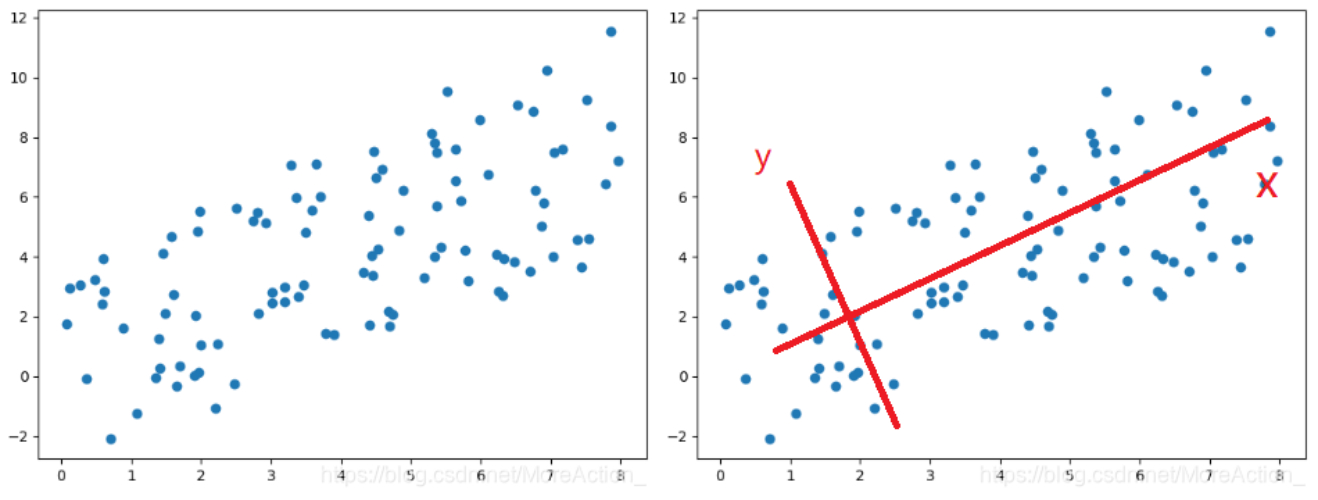
image-20250304103454934
旋转原始坐标系得到图中新的坐标系(红色表示)
可以看到，数据在x轴上的变化大，而在y轴变化小，变化小意味着数据在这个特征上没有太大的差异，因此可以忽略Y轴的数据，实现降维
PCA其实做的就是这么一件事，求出了一个正交矩阵P，然后用这个矩阵对数据进行正交变换得到新的数据：$ X_p = PX $

原理

度量信息量大小的方式：数据在某个轴上的分散程度即方差

先在整个数据空间中找到一个坐标轴（方向），使得数据在这个坐标轴上的投影（投影 = 坐标值）的方差达到最大，那么这个方向就是我们新的坐标系的第一个轴，然后再找一个方差次大的，而且与第一个轴垂直的方向（不限制垂直次大方向会和最大方向无限接近），作为新坐标系的第二个轴，依此类推，直到我们找出了 K 个，然后把原来的数据用这新的坐标系进行表示（也就是进行投影），就得到了降维后的数据。

数学推导

方差是每个元素与变量均值差的平方和的均值，一维数据的方差计算公式为：

\[ Var(a) = \frac{1}{m} \sum_{i=1}^{m} (a_i - \mu)^2 \]

为了后续计算方便，我们先进行去中心化操作（使数据均值为 0）。假设有 \(m\) 个 \(n\) 维数据，\(X = [x_1, x_2, ..., x_m]\)，其中的每个 \(x\) 是一个 \(n\) 维的列向量，去中心化：

\[ X = X - \frac{1}{m} \sum_{i=1}^{m} x_i \]

接下来，我们的目标就是在这个数据空间中找到一个方向，使得数据在这个方向上的投影的方差最大，假设这个方向为 \(w\)，\(\|w\|_2 = 1\)（单位向量），那么每个数据在这个方向下的坐标值为：\(w^T x_i\)，于是有方差：

\[ D(x) = \frac{1}{m} \sum_{i=1}^{m} (w^T x_i)^2 \]
\[ = \frac{1}{m} \sum_{i=1}^{m} (w^T x_i) (w^T x_i)^T \]
\[ = \frac{1}{m} \sum_{i=1}^{m} w^T x_i x_i^T w \]
\[ = w^T \left( \frac{1}{m} \sum_{i=1}^{m} x_i x_i^T \right) w \]

其中，\(\frac{1}{m} \sum_{i=1}^{m} x_i x_i^T\) 就是样本的协方差矩阵，令它为 \(C\)，那么我们的优化目标就是：

\[ \begin{cases} \max \{ w^T C w \} \\ \text{s.t. } w^T w = 1 \end{cases} \]

为了解这个约束优化问题，使用拉格朗日乘数法，构造拉格朗日函数 \(L\)：

\[ L(w, \lambda) = w^T C w + \lambda (1 - w^T w) \]

然后对每个分量求导，得到：

\[ \begin{cases} \frac{\partial}{\partial w} L(w, \lambda) = 2Cw - 2\lambda w = 0 \\ \frac{\partial}{\partial \lambda} L(w, \lambda) = w^T w - 1 = 0 \end{cases} \]

解得：

\[ \begin{cases} Cw = \lambda w \\ w^T w = 1 \end{cases} \]

这表明 \(w\) 是矩阵 \(C\) 的特征向量。将 \(w\) 代入目标函数中，得到：

\[ \max D(x) = \max \{ w^T C w \} = \max \{ w^T \lambda w \} = \max \lambda \]

因此，要找的最大方差就是协方差矩阵的最大特征值，而此时的方向就是最大特征值所对应的特征向量。次大方向自然是第二大特征值对应的特征向量，依此类推，直到我们找出了 \(K\) 个特征向量，以这 \(K\) 个特征向量作为新的坐标系，然后将原始数据投影到这个坐标系下即可得到降维后的数据。

论文内容

增量前沿信息结构

1、前言信息结构 (FIS)

创建新的前沿集群 \(F_i\) 时，计算前沿信息结构 \(FI_i\)，其包含的内容如下：

Data Explanation
\(C_i\) 集群的所有单元格
\(P_{avg,i}\) \(C_i\) 的平均位置
\(B_i\) 集群的轴对齐边界框
\(VP_i\) 候选监测点
\(L_{cost,i}\) \(F_i\) 与所有其他集群的连接成本

2、增量前沿检测和聚类

作用：更新地图

步骤：记录更新区域 \(B_m\) 的 AABB，遍历所有簇，返回与 \(B_m\) 相交的所有簇，检查返回簇，删去不是边界的簇。通过区域增长算法搜索新的边界并聚类，若最大特征超过阈值，先利用 PCA 降维 ( 沿第一个主轴分为两个簇 )。

image-20250306084257622

3、视点生成和成本更新

评论