空中机器人 ¶

约 3052 个字预计阅读时间 12 分钟

基本知识 ¶

定义 : 拥有自制和自主能力

分类 ¶

固定翼 - 机体结构、航电系统、动力系统、起降系统、地面控制站

旋翼

扑翼

气囊

伞翼

应用 ¶

无人机派送
消费级无人机

导航 ¶

定义：将运载体从起始点引导到目的地的技术或方法称为导航 (Navigation)

导航三大问题

我在那里
我要去哪里
我如何去

定位的本质是状态估计问题

飞行器的动态模型 ¶

坐标系与姿态转换 ¶

常见飞行器可以抽象为一个刚体。描述任意时刻的空间运动需要六个自由度：三个质心运动和三个角运动

地球中心坐标系(ECEF)

ECEF 坐标系与地球固联，位置在地球质心

WGS-84 坐标系

当前 GPS 所用的坐标系（地球是一个椭圆）

为什么不用 GPS 的海拔信息

GPS 的海拔高度不准

NED 坐标系

PID 技术 ¶

观看视频：PID 讲解

\(K_P\) 越大，控制系统的响应速度越大，但产生的震荡也越严重

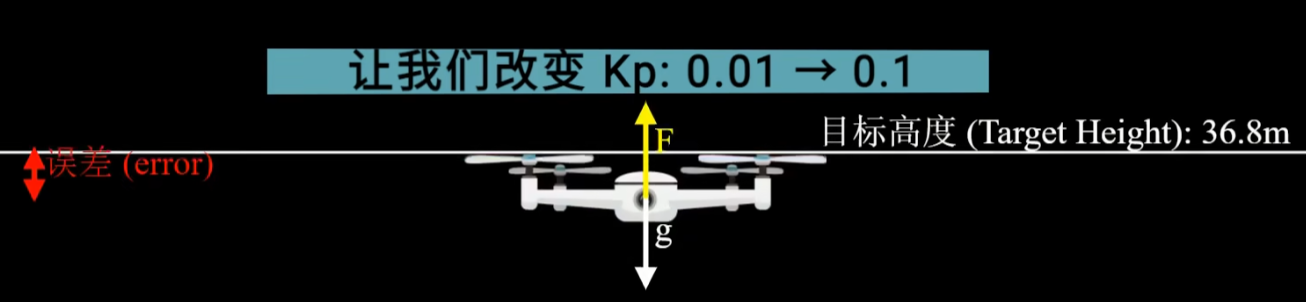
\(K_d\) 减缓震荡，但不能过大，否则会过冲

\(\frac{d(e)}{dt} = v\)，微分算法可以对无人机的速度发生响应

\(K_i\), 减小与目标位置之间的误差

轨迹规划 ¶

深度优先（DFS）¶

队列：先进后出

广度优先（BFS）¶

是没有权重的 Dijkstra 算法

队列：先进先出

广度优先搜索算法（BFS）

图示：

A 为起点，G 为终点。一开始我们在起点 A 上，此时并不知道 G 在哪里。

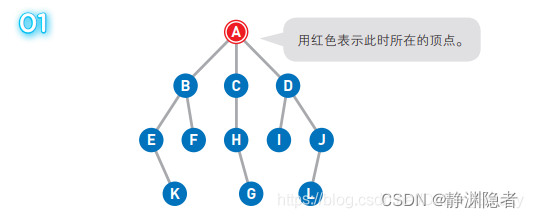
将可以从 A 直达的三个顶点 B、C、D 设为下一步的候补顶点。

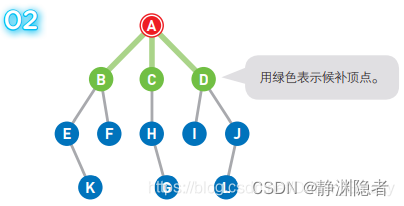
从候补顶点中选出一个顶点。优先选择最早成为候补的那个顶点，如果多个顶点同时成为候补，那么可以随意选择其中一个。

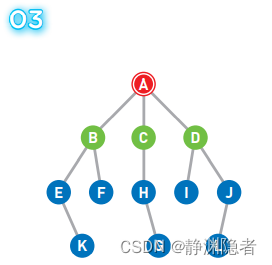
假设选择 B 点为先进去的，此时的队列 [B C D] 变为 [C D]

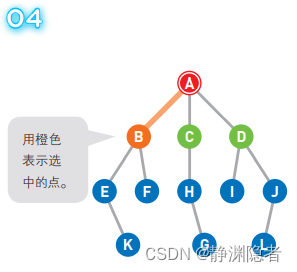
移动到选中的顶点 B 上。此时我们在 B 上，所以 B 变为红色，同时将已经搜索过的顶点变为橙色。

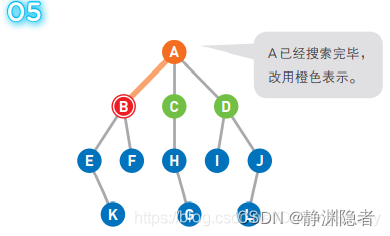
将可以从 B 直达的两个顶点 E 和 F 设为候补顶点并加入队列，变为 [C D E F]

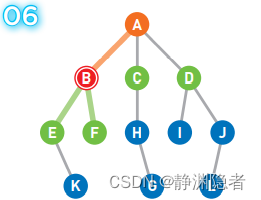
此时，最早成为候补顶点的是 C 和 D，我们选择了左边的顶点 C。

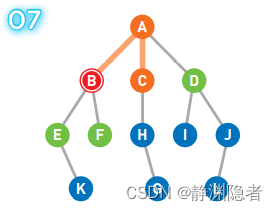
移动到选中的顶点 C 上。

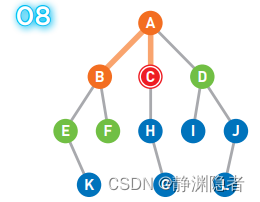
将可以从 C 直达的顶点 H 设为候补顶点，并将 C 移除队列，此时的队列 [D E F H]。

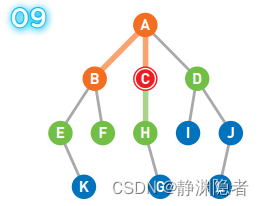
重复上述操作直到到达终点，或者所有的顶点都被遍历为止。

Dijkstra 算法 ¶

B 站视频

每次从未标记的节点中选取距离出发点最近的节点，标记，收录到最优路径集合中
计算刚加入节点 A 的邻近节点 B 的距离，若 A 的距离 +A 到 B 的距离小于 B 的距离，则更新 B 的距离

例题如下

首先用表格记录该店距离前面点的初始距离，起始的值都为无穷大，前面点都为空

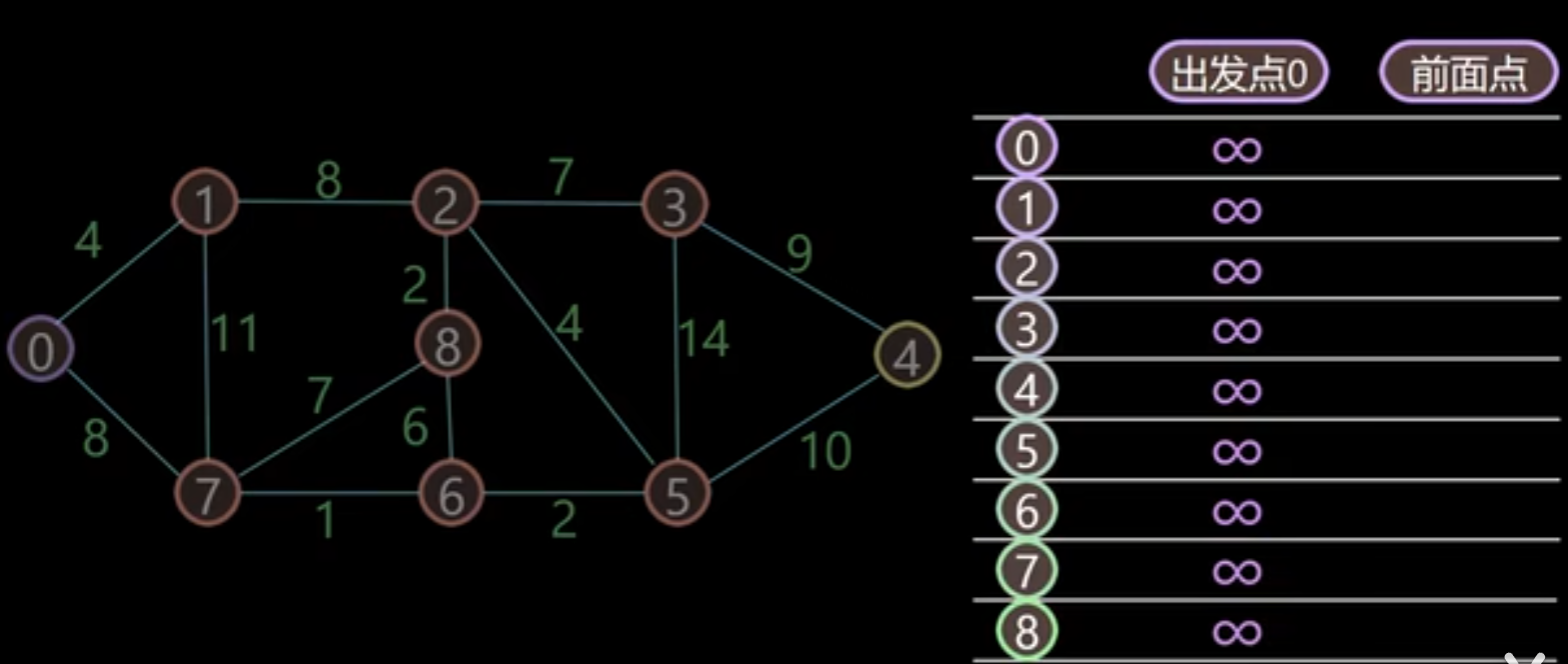
首先节点 0 到 0，距离为 0，找到距离最小的值，为 0，加入已搜索节点，并标注前面点为 0

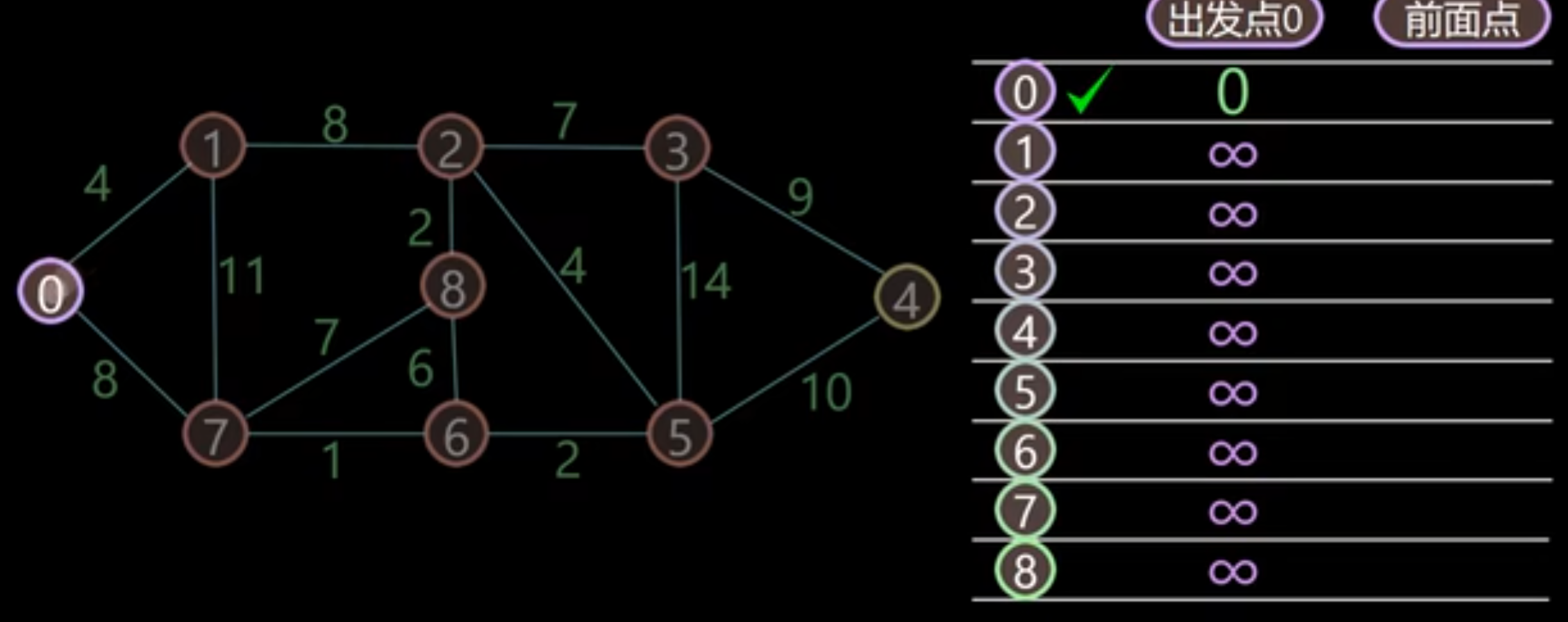
更新节点 0 附件的节点 1 和 7 的距离

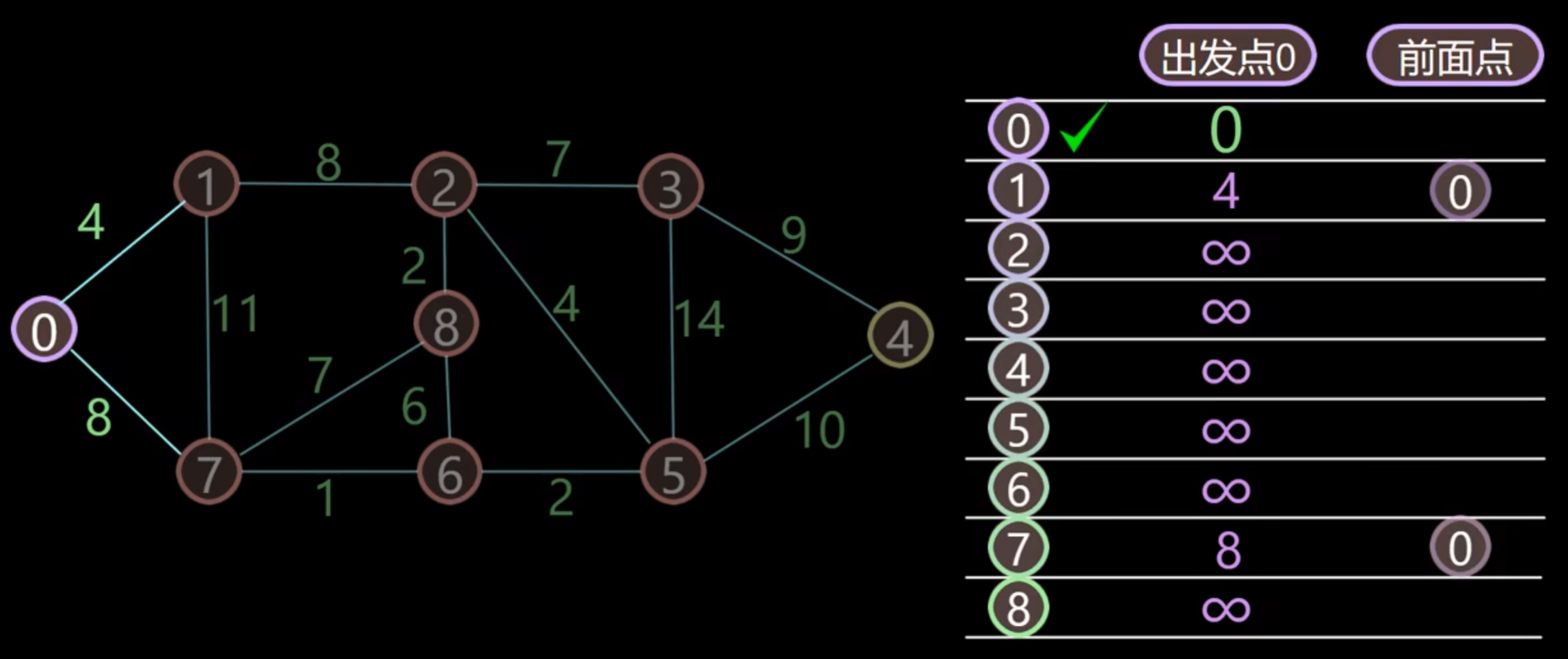
在未被加入已搜索节点的里面找到距离出发点最小的点，是 1 点，将其加入已搜索点，并跟新 1 节点周围的点的距离。

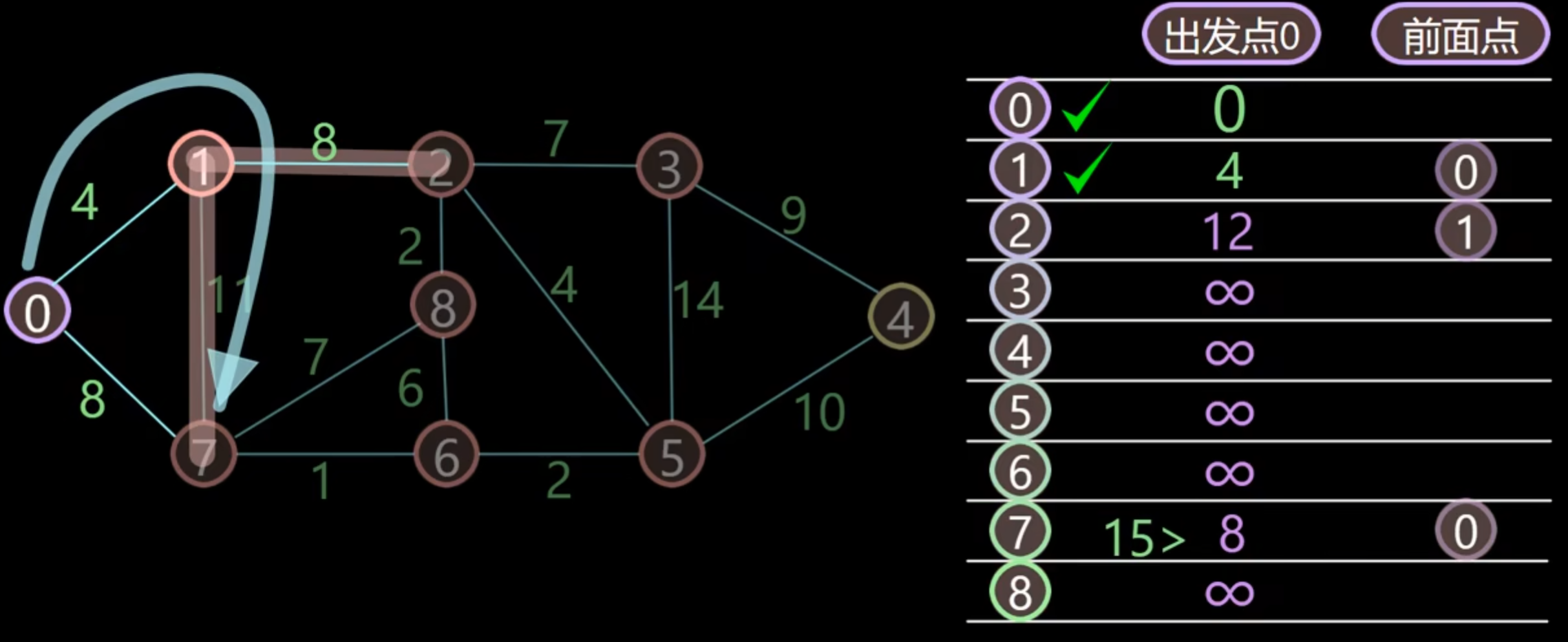
依次类推，直到所有点都被搜索完成

优点:

准确性: 总是能找到最短路径。
简单性: 实现相对简单。

缺点:

效率较低: 算法需要遍历图中的大多数节点，可能导致较高的计算成本。
实时性差: 在动态环境中可能不适用，因为它不能快速适应环境的变化

A* 算法 ¶

与 Dijkstra 的区别：是加了猜测 H 函数的 Dijkstra 算法

Dijkstra: G(n)
A*:F(n)=G(n)+H(n)

A* 讲解

搜索区域 (The Search Area) ¶

以题目进行解释，我们假设某人要从 A 点移动到 B 点，但是这两点之间被一堵墙隔开。如图 1 ，绿色是 A ，红色是 B ，中间蓝色是墙。

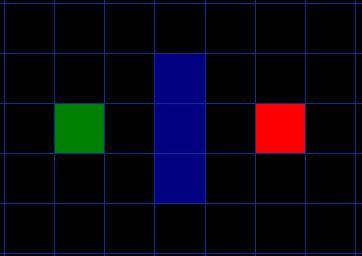
格子的状态分为可走 (walkalbe) 和不可走 (unwalkable)

开始搜索 (Starting the Search) ¶

从起点 A 开始，并把它就加入到一个由方格组成的 open list( 开放列表 ) 中。 Open list 里的格子是路径可能会是沿途经过的，也有可能不经过。基本上 open list 是一个待检查的方格列表。
查看与起点 A 相邻的方格 ( 忽略其中 unwalk 的方格 ) ，把其中可走的 (walkable) 或可到达的 (reachable) 方格也加入到 open list 中。把起点 A 设置为这些方格的父亲 (parent node 或 parent square) 。
把 A 从 open list 中移除，加入到 close list( 封闭列表 ) 中， close list 中的每个方格都是现在不需要再关注的。

如下图所示，深绿色的方格为起点，它的外框是亮蓝色，表示该方格被加入到了 close list 。与它相邻的黑色方格是需要被检查的，他们的外框是亮绿色。每个黑方格都有一个灰色的指针指向他们的父节点，这里是起点 A 。

路径排序 (Path Sorting) ¶

对每个节点，在计算时同时考虑两项代价指标：当前节点与起始点的距离，以及当前节点与目标点的距离：F = G + H

欧式距离：G = 从起点 A 移动到指定方格的移动代价，沿着到达该方格而生成的路径。
\(G = \sqrt{(x_1 - x_2)^2 +(y_1 - y_2)^2}\)
曼哈顿距离：H = 从指定的方格移动到终点 B 的估算成本。
\(H = |x_1 - x_2| + |y_1 - y_2|\)
注意，H 函数的选取要满足估算成本小于实际成本

计算起始点相邻方格的 F、G、H 的值，分别记录在左上角，左下角和右下角

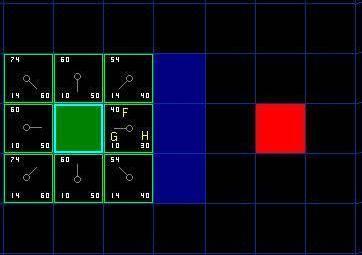
继续搜索 (Continuing the Search) ¶

为了继续搜索，我们从 open list 中选择 F 值最小的 ( 方格 ) 节点，然后对所选择的方格作如下操作：

把它从 open list 里取出，放到 close list 中。
检查所有与它相邻的方格，忽略其中在 close list 中或是不可走 (unwalkable) 的方格 ( 比如墙，水，或是其他非法地形 ) ，如果方格不在 open lsit 中，则把它们加入到 open list 中。把我们选定的方格设置为这些新加入的方格的父亲。
然后计算新加入的方格相对于当前处理方格的 F、G、H 值 ( 注意 G 为累加值 )
选取其中 F 值最小的作为下一个待处理的方格。
然后继续上面的操作。
如果某个相邻的所有方格均已经在 open list 中，则检查所有方格所在的这条路径是否更优，也就是说经由当前方格 ( 我们选中的方格 ) 到达那个方格是否具有更小的 G 值。
如果没有，不做任何操作。
相反，如果 G 值更小，则把那个方格的父亲设为当前方格 ( 我们选中的方格 ) ，然后重新计算那个方格的 F 值和 G 值。

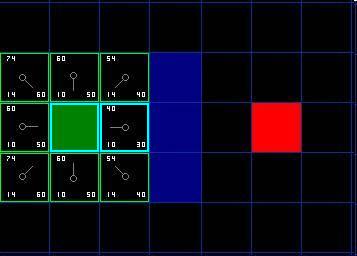
对于上图，在我们最初的 9 个方格中，还有 8 个在 open list 中，起点被放入了 close list 中。在这些方格中，起点右边的格子的 F 值 40 最小，因此我们选择这个方格作为下一个要处理的方格。它的外框用蓝线打亮。
首先，我们把它从 open list 移到 close list 中。然后我们检查与它相邻的方格。它右边的方格是墙壁，我们忽略。它左边的方格是起点，在 close list 中，我们也忽略。其他 4 个相邻的方格均在 open list 中，因此我们需要检查经由这个方格到达那里的路径是否更好，使用 G 值来判定。让我们看看上面的方格。它现在的 G 值为 14 。如果我们经由当前方格到达那里， G 值将会为 20。显然 20 比 14 大，因此这不是最优的路径。
当把 4 个已经在 open list 中的相邻方格都检查后，没有发现经由当前方格的更好路径，因此我们不做任何改变。现在我们已经检查了当前方格的所有相邻的方格，并也对他们作了处理，是时候选择下一个待处理的方格了。
因此再次遍历我们的 open list ，现在它只有 7 个方格了，我们需要选择 F 值最小的那个。有趣的是，这次有两个方格的 F 值都 54 ，选哪个呢？没什么关系。从速度上考虑，选择最后加入 open list 的方格更快。
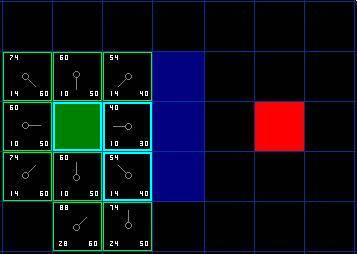
我们选择起点右下方的方格，如下图所示

只有三个方格可以选取，当前处理方格左边的方格，以及新加入的两个方格中。我们检查经由当前方格到达那里是否具有更小的 G 值。没有。因此我们准备从 open list 中选择下一个待处理的方格。
以此类推，找到最短路径

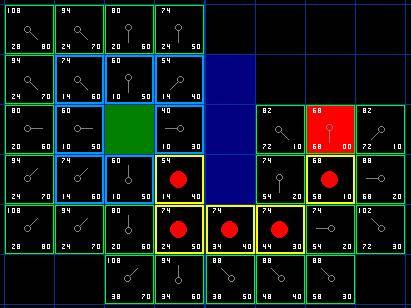
JPS 算法 ¶

实验课程 ¶

树莓派密码:
pi

主线任务——设置位置控制器，实现无人机悬停 ¶

线性控制器 ¶

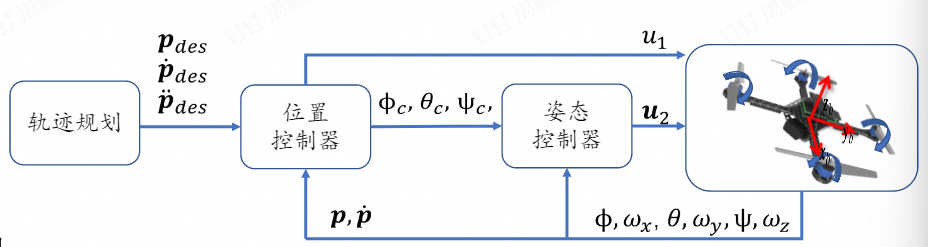
采用串级 PID 控制，内层控制姿态，外层控制位置。

模型构建 ¶

线性化

平衡悬停态： \((\phi_0 \sim 0, \theta_0 \sim 0, u_{1,0} \sim mg)\)

牛顿方程：

\[ m\ddot{p} = \begin{bmatrix} 0 \\ 0 \\ -mg \end{bmatrix} + R \begin{bmatrix} 0 \\ 0 \\ F_1 + F_2 + F_3 + F_4 \end{bmatrix} \]

\[ 其中R = \begin{bmatrix} c\psi c\theta - s\phi s\psi s\theta & -c\theta s\psi & c\psi s\theta + c\theta s\phi s\psi \\ c\theta s\psi + c\psi s\phi s\theta & c\phi c\psi & s\psi s\theta - c\theta c\phi s\phi \\ -c\theta s\theta & s\phi & c\theta c\phi \end{bmatrix} \]

\[ 在小角度近似的情况下，得到\begin{cases} \ddot{p}_1 = \ddot{x} = g(\theta c\psi + \phi s\psi )\\ \ddot{p}_2 = \ddot{y} = g(\theta s\psi - \phi c\psi) \\ \ddot{p}_3 = \ddot{z} = -g + \frac{u_1}{m} \end{cases} \]

欧拉角微分：

\[ \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} = \begin{bmatrix} c\theta & 0 & -c\phi s\theta \\ 0 & 1 & s\phi \\ s\theta & 0 & c\phi s\theta \end{bmatrix} \begin{bmatrix} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{bmatrix} \]

线性化后

\[ \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} = \begin{bmatrix} u_2 \\ u_3 \\ u_4 \end{bmatrix} \]

欧拉方程：

\[ I\cdot \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} + \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} \times I \cdot \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} = \begin{bmatrix} u_{2x} \\ u_{2y} \\ u_{2z} \end{bmatrix} - \begin{bmatrix} l(F_2 - F_4) \\ l(F_3 - F_1) \\ M_1 - M_2 + M_3 - M_4 \end{bmatrix} \]

PID 控制

位置控制

\[ \ddot{p}_{i,c} = \ddot{p}_i^{des} + K_{d,i}(\dot{p}_i^{des} - \dot{p}_i) + K_{p,i}(p_i^{des} - p_i) \\ \]

由上述方程可以求出 \(p_{i,c}\)
再带入牛顿方程的解的到预期的 \(\phi_c\)、\(\theta_c\) 和 \(u_1\)
\(\phi_c = \frac{1}{g}(\ddot{p}_{1,c}s\psi - \ddot{p}_{2,c}c\psi)\)
\(\theta_c = \frac{1}{g}(\ddot{p}_{1,c}c\psi + \ddot{p}_{2,c}s\psi)\)
\(u_1 = m(g + \ddot{p}_{3,c})\)

姿态控制

PID 控制

\[ \begin{bmatrix} \ddot{\phi}_c \\ \ddot{\theta}_c \\ \ddot{\psi}_c \end{bmatrix} = \begin{bmatrix} K_{p,\phi}(\phi_c - \phi) + K_{d,\phi}(\dot{\phi}_c - \dot{\phi}) \\ K_{p,\theta}(\theta_c - \theta) + K_{d,\theta}(\dot{\theta}_c - \dot{\theta}) \\ K_{p,\psi}(\psi_c - \psi) + K_{d,\psi}(\dot{\psi}_c - \dot{\psi}) \end{bmatrix} \]

模型

\[ u_2 = I \begin{bmatrix} \ddot{\phi}_c \\ \ddot{\theta}_c \\ \ddot{\psi}_c \end{bmatrix} + \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} \times I \begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} \]

代码逻辑 ¶

位置控制器 ¶

输入输出

输入：\(p_des\)、\(\dot{p}_des\)、\(\ddot{p}_des\) 以及当前的 yaw 角
输出：当前的位置\(P_c\),预期的roll、Pitch角
返回：当前的yaw与预期的roll、Pitch计算的新的四元素给姿态控制器

imu.q              -> Euler
Euler.yaw P_des    -> P_c roll_d pitch_c
yaw pitch_c roll_c -> u.q(输出)